Как найти небо на фотографии?
Мне интересно компьютерное зрение и всё что с ним связано, и я решил поиграться с одной из технологий, вычитанной из этой статьи. С самого начала хотелось выводить на фотографию с небом космический корабль типа Thunderhawk, который пролетает мимо или просто взлетает. Но от этого пришлось отказаться, у меня нет модельки, знаний, как правильно рассчитать перспективу и понять, как правильно считать освещение. Взяв статью, я не обратил внимания, что она только для наземных роботов. Авторы статьи упростили себе работу, сделав распознавание только для наземных роботов. Раз робот наземный, то все, что наверху - у него небо, и допущение, которое использует алгоритм, - это то, что мы начинаем сверху сканировать изображение и считаем всё, что находится вверху небом.
Для начала мы строим границы градиентов с помощью свёртки по оператору Собеля. Операция свёртки - это базовая операция в компьютерном зрении. Мы проходимся по каждому пикселю в изображении, берем его значение и значения близко расположенных пискелей. Складываем их вместе, умножая на множители из ядра. Ядро Собеля состоит из двух частей X и Y. В конце мы собираем значение вместе через евклидово расстояние.
За евклидовым расстоянием на самом деле прячется простая формула нахождения стороны треугольника с помощью теоремы Пифагора. Фокус заключается в том, что мы не можем брать одну меру от двух мер. Так как x и y - это две размерности, которые между собой не связаны. А вот эту получившуюся меру мы берём как точку в новом пространстве.
В зависимости от режима цвета, с которым мы работаем с изображением, числа в свёртке будут меняться. Авторы статьи не указали, в каком режиме они обрабатывали это изображение. Говорится только о пороге, равном 600 и максимальном 1770, это ничего не говорит о цветности, которую они использовали. При тестировании я получил лучшие результаты на серых изображениях, либо на изображениях, на которых используются красный и зелёный канал вместе. Теперь имеем картинку с порогами перехода между цветами в изображении. Пороги при этом у нас просто числа, а никакой не цвет. Данные картинки демонстрируют оператор Собеля по X и Y на области изображения с границей и градиентом.






Теперь, имея эту картинку с допусками, мы начинаем спускаться вниз по изображению по каждой линии вверх-вниз, перебирая, на каком пороге остановиться сейчас. На каждом шаге спуска мы пересчитываем энергетическую функцию изображения. Там где энергетическая функция максимальна проходит граница между небом и землей на изображении. Мы её пересчитываем каждый раз, потому что делим всю картинку на небо и землю, и каждый участок в энергетической функции - это своя переменная в функции. Чем меньше у нас знаменатель, тем больше энергетическая функция. Функция представляет из себя сумму определителей ковариационных матриц участков земли и неба, сложенную с суммой собственных векторов этих участков. Чем у нас однообразней участок, тем меньше у него определитель, а собственный вектор стремится к нулю при общей однообразности. Так как на земле обычно большее разнообразие, то её определитель будет больше, что будет давать меньшее значение у энергетической функции.
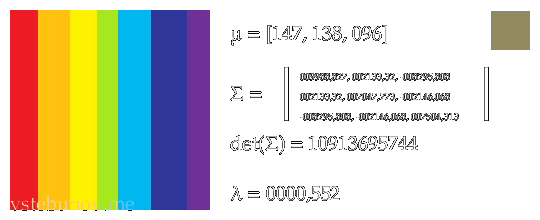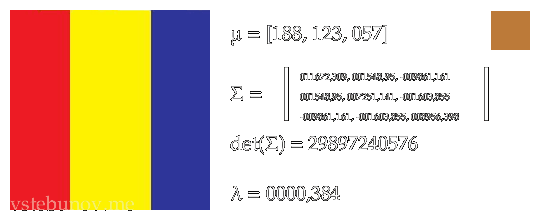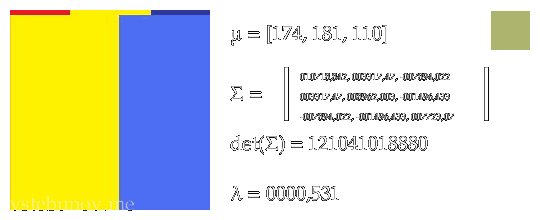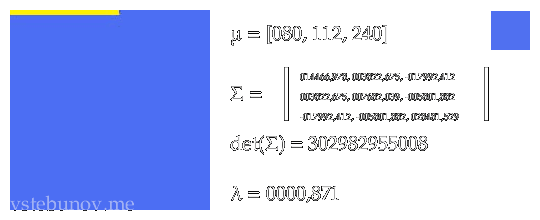
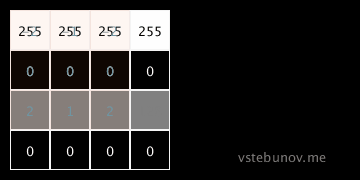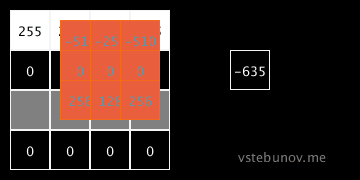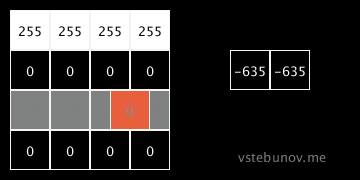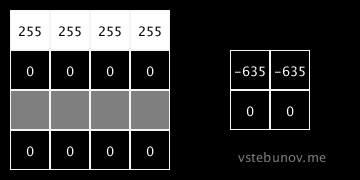
Ингридиенты энергетической функции без разделения на небо и землю.
Слева-направо.
1. Изображение из которого мы рассчитываем.
2. μ - средний цвет.
3. Σ - ковариационная матрица.
4. det(Σ) - определитель ковариационной матрицы
5. λ - первое число собственного вектора.
6. В правом квадрате средний цвет области.Там где необходимо взяты абсолютные значения.
Далее идет правка ошибок: если картина не содержит неба совсем или часть картинки начинается не с неба, то эту часть мы удаляем с помощью алгоритма кластеризации. Но мне не очень был интересен этот алгоритм, поэтому вдаваться в него я не стал.
Последним шагом мы рисуем картинку и по тем местам, где граница и выше, кислотное небо. Эффект кислотного неба достигается тем, что мы берём шум Перлина и заменяем цвета на заданные заранее из выборки. После чего смещаем индекс в выборке, таким образом достигается эффект движения кислотного неба. Первый раз я такой эффект увидел в старой программе скринсейвере еще под dos, только там это всё выполнялось на фракталах или простых картинках.
Что получилось?
На картинке из сходной статьи у меня всё отрабатывает чётко и правильно. Отладка - это самое сложное, и я боялся, что ошибка окажется в энергетической функции. По итогам ошибки были в операторе Собеля. Я разобрался в языке Processing, и он мне понравился как инструмент для генерации картинок и их обработки.
Что не получилось?
Не получилось, что задумывалось: выводить точную границу неба. Потому что допущение того, что небо всегда сверху не всегда правдиво. Второй момент - я не умею находить, насколько нужно размывать границу перехода между небом и землей, без этого картинки не такие интересные. Третий момент - при маленькой границе допуска небо может “протечь” на землю в тех местах, где истончается наш порог, но при этом земля остается достаточно однородной. Либо небо может, наоборот, не дойти до границы, потому что резкий переход градиента между облаком и небом не даёт алгоритму спуститься ниже. Четвертое - это интеграция с 3D, которая была отложена и не сделана.
Что можно улучшить?
Возможно, необходимо делать границы одного допуска одинаковыми по значению допуска с помощью какого-то алгоритма. Возможно, следует добавить отражение свечения неба на земле. Необходимо найти алгоритм правильного размывания границ для конечного вывода.
Результат
И картинки из моих фотографий.


Ссылка: